

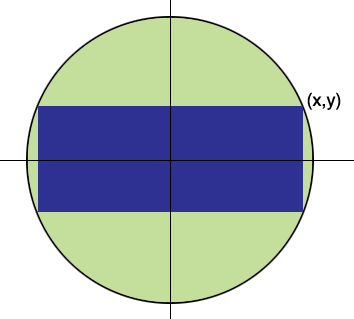
Then the word inscribed means that the rectangle has two vertices on the semicircle and two vertices on the x axis as shown in the top. Well, if that rectangle was bigger than all the other rectangles and the line segments, it's certainly bigger than all the other rectangles, and you have your answer. EXAMPLE 5 Find the area of the largest rectangle that can be inscribed in a semicircle of radius r SOLUTION 1 Let's take the semicircle to be the upper half of the circle x, + y,r, with center the origin. And it turns out that this maximum occurs at a value of $x$ that produces a non-degenerate rectangle, not just a line segment.
And you find the maximum value of $A(x)$ on this entire set.

with no value of $x$ where $A(x)$ matches or exceeds all other values of $A(x).$īut if you decided that instead of looking only at non-degenerate rectangles (the kind that have two dimensions and seem to you to be legitimate rectangles), you will look at this class of shapes that include some line segments (produced when $x=0$ or $x=2$) as well as non-degenerate rectangles. If you were just doing $x \in (0,2),$ it's conceivable that for some way of generating shapes with that parameter, there's a local maximum at $x = 1,$ but $A(0.1) > A(1),$ $A(0.01) > A(0.1),$ etc. 3 Answers Sorted by: 0 If you impose that a rectangle must have width and length greater than 0 0, then your argument can be used to prove that there is no smallest rectangle in the given conditions. Such examples use closed intervals because as long as $A(x)$ (or whatever you're trying to maximize) is defined everywhere and is continuous on the interval, it has a maximum value in the interval. To find the maximum, take the derivative and set it equal. So then, I can make Z a function of one variable by substituting from the circle equation, So now I have a function of one variable. This allowed me to come to the conclusion, using the pythagorean theorem, that the height of the trapezoid is $h=\sqrt. Thats the same solution as the area because if the area is the maximum, then the square of that area will also be the maximum. The problem of determining the area of the largest rectangle inscribed in a semicircle was solved by introducing a coordinate system whose origin is the center of the semicircle. Let r be the radius of the semicircle, x one half of the base of the rectangle, and y the height of the rectangle. Examples: Input : r 4 Output : 16 Input : r 5 Output :25. Denote this length as 8, the radius of the semicircle. I outlined the rectangle within the trapezoid and the two right triangles within it. Given a semicircle of radius r, we have to find the largest rectangle that can be inscribed in the semicircle, with base lying on the diameter. Draw two lines from that center to the point where the rectangle intersects the arc of the semicircle.

Let 0 be the angle shown in the bottom figure. calculates to 48 when given numerical values are plugged in. Rectangle area is obtained by multiplying the above. Solve 1) and 2) x1 ka 2, y1 kb 2 x 1 k a 2, y 1 k b 2. Therefore the area of the largest inscribed rectangle is A (-) 2 V2 V2 SOLUTION 2 A simpler solution is possible we think of using an angle as a variable. The ellipse is intersected by a pair of straight lines. YA EXAMPLE 5 Find the area of the largest rectangle that can be inscribed in a semicircle a of radius r. I drew out a circle with a radius of 1 and drew a trapezoid inscribed in the top portion of it. This value of x gives a maximum value of A since A (0) 0 and A (r) 0. The formula for the area, A, of a circle is built around its radius.


 0 kommentar(er)
0 kommentar(er)
